Teste t de Student bilateral para uma média com variância desconhecida

Deixe um comentário / blog, teste-t-student, tutorial / Por

Neste artigo você irá aprender a aplicar o teste t de Student para comparar uma média, que tem distribuição Normal e a variância é desconhecida, com um valor esperado, especificado ou conhecido.

Existem vários tipos de testes de comparação de médias, sendo que o teste t de Student é um dos mais utilizados. Isto se deve basicamente a:

  • Seu cálculo é simples;
  • As premissas não são muito complexas;
  • Está implementado na grande maioria dos softwares de análise de dados, isso se não for em todos.

Porém, existem vários tipos de teste t de Student que variam de acordo com o que se deseja comparar e também em qual é a relação das variâncias envolvidas. Por isto, é importante ter conhecimento de como estes testes são conduzidos, tanto do ponto de vista teórico como também as principais etapas de cálculo que estão envolvidas na aplicação do teste.

Índice

Este teste deve ser utilizado quando queremos saber se uma média proveniente de uma distribuição Normal, e que tem variância desconhecida, é diferente de um valor conhecido e/ou esperado.

Conjunto de dados

A Tabela 1 traz dados de concentração de Potássio (K) quantificadas em 7 amostras aleatórias bananas. A concentração esperada para a variedade avaliada é de 374 mg/100g.

Tabela 1: Concentração de potássio em bananas.

Amostra Ordem de coleta Concentração de K (mg/100g)
1 1 369
2 5 368
3 3 367
4 4 388
5 6 379
6 2 371
7 7 399

Caracterização da amostra

  • $\overline{x} = 377,29 \;mg/100g$;
  • $n=7$;
  • $gl=6$;
  • $s = 12,175 \;mg/100g$;
  • $s^{2} = 148,238 \;mg^2/\left(100g\right)^{2}$;
  • $s_{x} = 4,602\;mg/100g$;
  • $s_{IC,\alpha=0,05} = 11,230\;mg/100g$;
  • $IC_{inferior} = 366,025\;mg/100g$;
  • $IC_{superior} = 388,546\;mg/100g$;
  • Distribuição Normal? Falha em rejeitar $H_{0}$ (Sim);

Premissas

O teste t de Student bilateral para uma média amostral tem os seguintes pressupostos:

  • A amostra segue, pelo menos aproximadamente, a distribuição Normal

    Como é avaliado um conjunto de dados em envolve a concentração de um composto em bananas de uma mesma variedade, este pressuposto é bastante aceitável. Apesar do baixo tamanho amostral ($n=7$), o teste de Normalidade de Shapiro-Wilk indica que o conjunto segue a distribuição Normal ($p-valor=0,112$).

  • A variância da população é desconhecida.

    Neste caso não temos informação sobre a variância da concentração de potássio nas bananas, e a variância é estimada a partir dos dados experimentais;

  • Não existem outliers;

    Admitimos que os experimentos foram conduzidos seguindo os protocolos adequados e o conjunto de dados não apresenta outliers.

  • A amostragem foi realizada de forma aleatória

    A amostragem destes dados foi realizada de forma aleatória, sendo que temos informação sobre a ordem (Tabela 1) em que cada amostra foi coletada/analisada.

Assim, consideramos que os dados experimentais atendem aos pressupostos do teste t de Student bilateral para uma média amostral.

Hipóteses

O teste t de Student bilateral para comparar uma média amostral com um valor verdadeiro/esperado parte da premissa que a média da amostra é igual ao valor esperado, e a hipótese alternativa contesta esta hipótese adotando que a média é diferente do valor esperado. Ou seja:

$$
\begin{cases}H_{0}: & \mu = \mu_{0}\\H_{1}: & \mu \neq \mu_{0}\end{cases}
$$

onde:

  • $\mu$ é a média verdadeira da amostra;
  • $\mu_{0}$ é o valor esperado para a amostra;

Hipóteses levantadas

Como hipótese nula adotamos que a concentração de potássio média da amostra aleatória de bananas é igual ao valor esperado para esta fruta. Assim:

$$
H_{0}: \mu = \mu_{0} \longrightarrow 377,29 = 374
$$

A hipótese alternativa contesta a hipótese nula. Ou seja:

$$
H_{1}: \mu \neq \mu_{0} \longrightarrow 377,29 \neq 374
$$

Estatística do teste t de Student​

O teste t de Student para comparar uma média com um valor conhecido/esperado é definido através da Equação 1.

$$ t_{0}=\frac{\left( \overline{x} – \mu_{0} \right)\sqrt{n}}{s} $$

(1)

onde:

  • $\overline{x}$ é a média da amostra;
  • $\mu_{0}$ é o valor esperado ou conhecido para a média;
  • $n$ é o número total de observações;
  • $s$ é o desvio padrão da amostra;
  • $t_{0}$ é a estatística do teste.

Cálculo da estatística

Para estimar a estatística do teste, basta substituir os dados da amostra na Equação 1. Adotando $\mu_{0}=374\;mg/100g$, temos:

$$
t_{0}=\frac{\left( \overline{x} – \mu_{0} \right)\sqrt{n}}{s}=\frac{\left( 377,29 – 374 \right)\sqrt{7}}{12,17}=0,714
$$

Grau de liberdade

O número de graus de liberdade é o número de observações utilizadas no cálculo final de uma estatística que podem variar livremente. Como este teste é para uma amostra, perdemos um (1) grau de liberdade (Equação 2).

$$
gl=n-1
$$

(2)

Cálculo do grau de liberdade

A estimativa do grau de liberdade é feita substituindo o tamanho amostral na Equação 2:

$$
gl=n-1=7-1=6
$$

Valor crítico da distribuição t de Student

O valor crítico é obtido da distribuição t de Student bilateral com $n-1$ graus de liberdade (Equação 3).

$$ t_{critico}=t_{1-\alpha/2;\;n-1} $$

(3)

Geralmente adotamos o valor crítico superior ($1-\alpha/2$) pois é um valor positivo (cauda direita). O valor crítico inferior ($\alpha/2$) tem o mesmo valor que o anterior, porém seu sinal é negativo (cauda esquerda).

Obtenção do valor crítico

O valor crítico do teste é obtido com:

$$ t_{critico}=t_{1-\alpha/2; \;n-1}=t_{1-0,05/2; \;7-1}=t_{0,975;\;6} $$

Tais valores críticos podem ser encontrados em Tabelas da distribuição t de Student (Tabela 2).

Tabela 2: Valores críticos da distribuição t de Student bilateral.

Nível de significância
gl 0,10 0,05 0,01
1 6,314 12,706 63,657
2 2,920 4,303 9,925
3 2,353 3,182 5,841
4 2,132 2,776 4,604
5 2,015 2,571 4,032
6 1,943 2,447 3,707
7 1,895 2,365 3,499
8 1,860 2,306 3,355
9 1,833 2,262 3,250
10 1,812 2,228 3,169

Para obter o valor crítico basta observar a coluna com o nível de significância estabelecido e a linha com o grau de liberdade do teste. Neste caso, estamos adotando $\alpha=0,05$ e temos $gl=6$. Portanto, $t_{critico}=2,447$.

Existem tabelas para o teste bilateral e tabelas para o teste unilateral.

Probabilidade

A probabilidade ($p-valor$) do teste é estimada combinando a estatística do teste ($t_{0}$) com a distribuição t de Student. Para o teste bilateral, a probabilidade é estimada utilizado a Equação 4:

$$ p-valor=2P\left(T_{n-1}>|t_{0}|\right) $$

 

(4)

Obtenção do p-valor

Podemos utilizar as tabelas da distribuição t de Student para obter a probabilidade do teste (Tabela 2). Porém, devemos procurar na linha com o grau de liberdade do teste, qual valor é mais próximo do da estatística do teste ($t_{0}$). Observando a linha para $gl=6$ na Tabela 2, o valor mais próximo de $t_{0}=0,714$ é $1,934$ na coluna para $\alpha=0,10$. Assim, podemos concluir que o $p-valor$ do teste é maior do $0,10$. Se tivermos acesso a uma tabela com mais informações, como esta tabela (simplificada na Tabela 3), iriamos obter que $0,714$ esta entre $0,718$ ($\alpha=0,5$) e $0,553$ ($\alpha=0,6$).

Tabela 3: Valores críticos da distribuição t de Student bilateral.

Nível de significância
gl 0,40 0,50 0,60
1 1,376 1,000 0,727
2 1,061 0,816 0,617
3 0,978 0,765 0,584
4 0,941 0,741 0,569
5 0,920 0,727 0,559
6 0,906 0,718 0,553
7 0,896 0,711 0,549
8 0,889 0,706 0,546
9 0,883 0,703 0,543
10 0,879 0,700 0,542

Portanto, o $p-valor$ do teste esta entre $0,553$ e $0,718$.

Conclusão do teste

A conclusão do teste pode ser feita comparando a estatística do teste com o valor crítico ou comparando a probabilidade estimada com o nível de significância. As duas opções fornecem exatamente o mesmo resultado.

Comparando o valor crítico ($t_{critico}$) com a estatística do teste ($t_{0}$)

  • Se $|t_{0}| > t_{critico}$, rejeitamos a hipótese nula ($\overline{x}\neq\mu_{0}$);

  • Se $|t_{0}| \leq t_{critico}$, falhamos em rejeitar a hipótese nula ($\overline{x} = \mu_{0}$)

Concluindo o teste

Como a estatística do teste ($t_{0}=0,714$) é menor do que o valor crítico ($t_{critico}=2,447$), falhamos em rejeitar a hipótese nula (com $95\%$ de confiança). Portanto, a concentração da potássio nas bananas é igual ao valor esperado.

Comparando a probabilidade ($p-valor$) com o nível de significância adotado ($\alpha$)

  • Se $p-valor < \alpha$, rejeitamos a hipótese nula ($\overline{x}\neq\mu_{0}$);

  • Se $p-valor \geq \alpha$, falhamos em rejeitar a hipótese nula ($\overline{x} = \mu_{0}$)

Concluindo o teste

Como $p-valor$ do teste ($0,553\leq p-valor\leq0,718$) é maior do que o nível de significância adotado ($\alpha=0,05$), falhamos em rejeitar a hipótese nula (com $95\%$ de confiança). Portanto, a concentração da potássio nas bananas é igual ao valor esperado.

Gráfico da distribuição t de Student

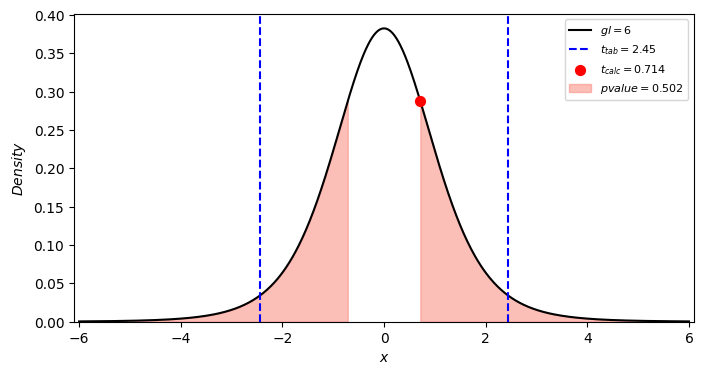
Visualmente, temos o seguinte resultado do teste como apresentado na Figura 1:

Figura 1: Gráfico da distribuição t de Student bilateral

Gráfico da distribuição t de student para seis graus de liberdade, com a área bilateral preenchida na cor salmão, valores críticos delimitando o ponto de decisão do teste na cor azul e o ponto com o valor da estatística em vermelho, indicando que o teste falha em rejeitar a hipótese nula.

Análise dimensional da estatística do teste

Assumindo que a amostra tem unidade de $cm$, temos que:

  • $\overline{x} \longrightarrow mg/100g$ ;
  • $\mu_{0}\longrightarrow mg/100g$;
  • $n\longrightarrow admensional$;
  • $s\longrightarrow mg/100g$;

Substituindo as unidades na Equação 1:

$$ t_{0}= \frac{\left( \overline{x} – \mu_{0} \right)\sqrt{n}}{s} = \frac{\left( mg/100g – mg/100g \right)\sqrt{admensional}}{mg/100g} = \frac{\left( mg/100g \right)\cancel{\sqrt{admensional}}}{mg/100g} = \frac{\cancel{mg/100g}}{\cancel{mg/100g}} = admensional $$

Portanto, a estatística do teste ($t_{0}$) é adimensional.

Conclusão Geral

Neste artigo vimos como aplicar o teste t de Student para comparar uma média com um valor especificado. A conclusão é que, com o conjunto de dados utilizado, não encontramos evidências para rejeitar a hipótese nula (média é igual ao valor esperado) quando avaliamos a hipótese alternativa (média é diferente do valor esperado).

Além disto, vimos como este teste é realmente simples, e não faz uso de nenhum cálculo complexo, uma vez que a parte trabalhosa já esta tabelada.

Saiba mais

Embora seja bem simples fazer os cálculos demonstrados acima, o ideal é trabalhar com softwares para minimizar as chances de erro. Os links que seguem utilizam o mesmo conjunto de dados adotado neste exemplo, fazendo os cálculos de forma mais direta e utilizando diferentes softwares.

Referências

STUDENT. The Probable Error of a Mean. Biometrika, v. 6, n. 1, p. 1, mar. 1908. DOI: https://doi.org/10.2307/2331554.

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *