Em um post anterior, estudamos como aplicar o teste t de Student com detalhes, porém, de forma arcaica numérica . Neste post vamos aplicar o teste t para uma média com Excel.
Neste artigo você encontra:
A planilha foi desenvolvida utilizando a versão 2019 do Microsoft Excel.
Cálculo da estatística
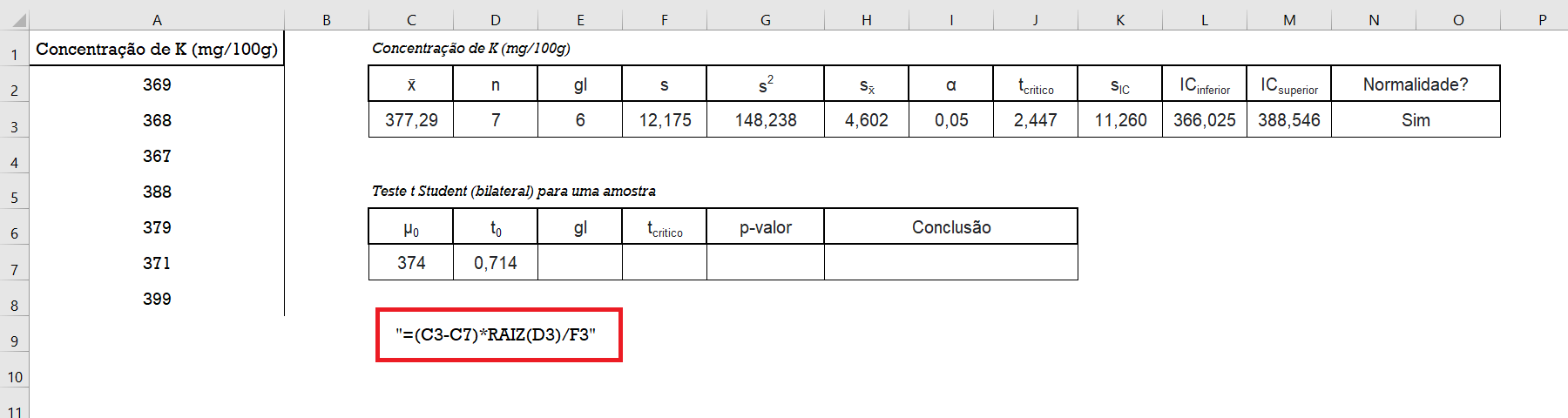
Dado que a média da amostra ($\overline{x}$) esta na célula C3, o valor esperado ($\mu_{0}$) esta na célula C7, o número de observações da amostra ($n$) esta na célula D3 e que o desvio padrão amostral (s) esta na célula F3, a estatística do teste ($t_{0}$) é estimada utilizando a seguinte fórmula:
=(C3-C7)*RAIZ(D3)/F3 0,714
Grau de liberdade
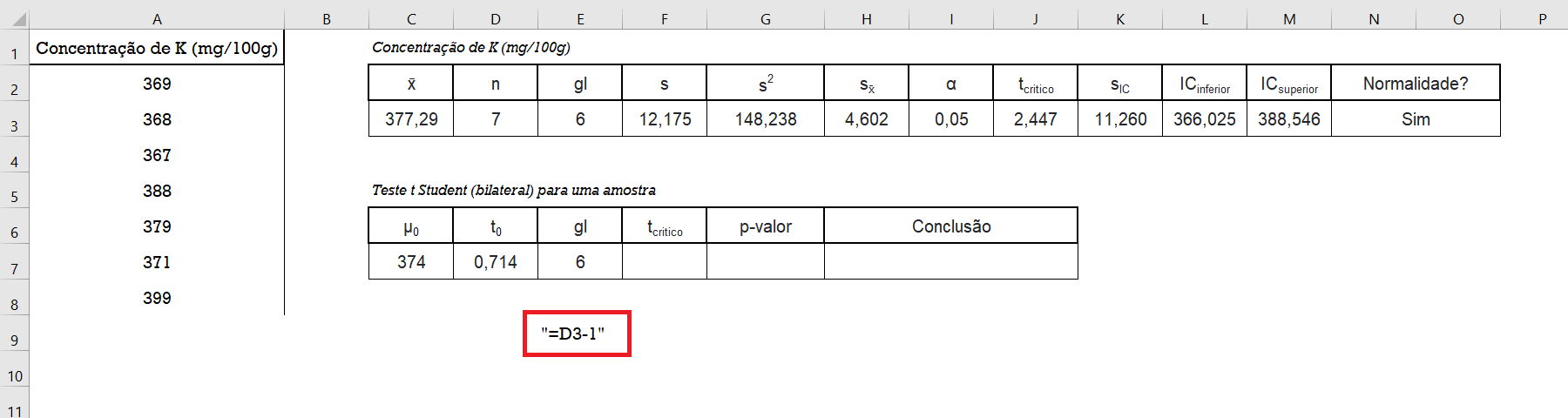
Dado que o tamanho da amostra ($n$) esta na célula D3, o grau de liberdade é estimado utilizando a seguinte fórmula:
=D3-1 6
Obtenção do valor crítico
Podemos obter o valor crítico bilateral utilizando o Excel utilizando a função =INV.T.BC(). Esta função retorna diretamente o valor bilateral da cauda direita (veja mais detalhes na documentação). Ela deve receber dois parâmetros:
- O primeiro é o nível de significância ($\alpha$);
- O segundo parâmetro é o grau de liberdade da amostra, $n-1=7-1=6$.
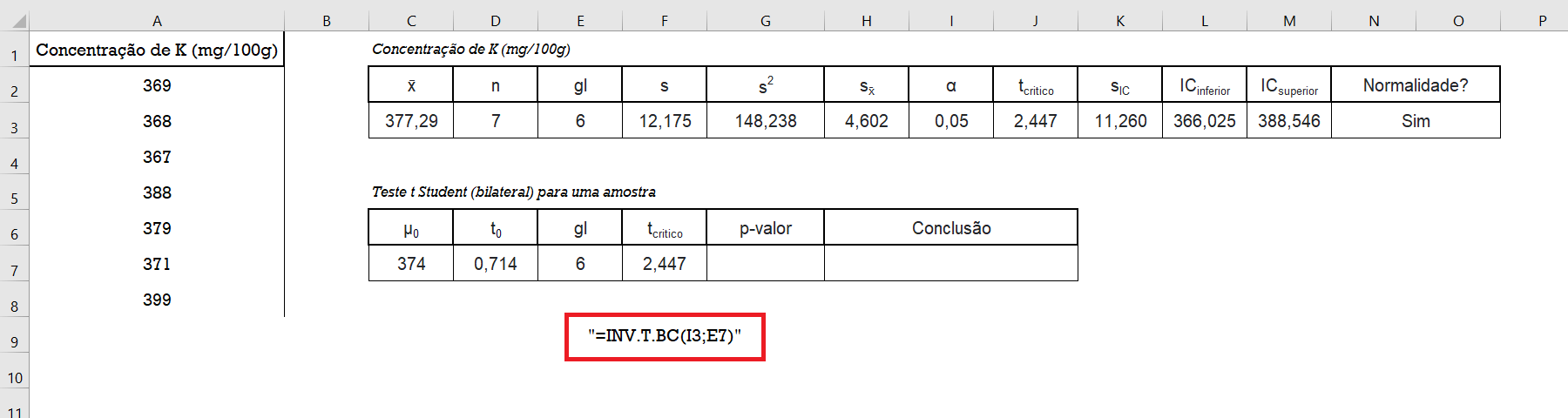
A principal vantagem desta função é que os valores críticos são da distribuição bilateral (ao contrário da função =INV.T(), que é unilateral). Dado que o nível de significância do teste ($\alpha$) esta na célula I3 e que o grau de liberdade da amostra ($gl$) esta na célula E7, o valor crítico é obtido utilizando a seguinte fórmula:
=INV.T.BC(I3;E7) 2,447
Obtenção do p-valor
A probabilidade do teste é obtida utilizando a estatística do teste ($t_{0}$) e o grau de liberdade da amostra. Podemos obtê-la facilmente utilizando o Excel utilizando a função DIST.T.BC().
A função DIST.T.BC() retorna diretamente o p-valor para a distribuição bicaudal (veja detalhes na documentação). Ela recebe dois parâmetros:
- O primeiro é a estatística do teste, com o detalhe que a estatística deve ser um valor positivo. Assim, passamos o valor absoluto estimado para a estatística, $|t_{0}|=|0,714|=0,714$;
- O segundo parâmetro é o grau de liberdade da amostra, $n-1=7-1=6$.
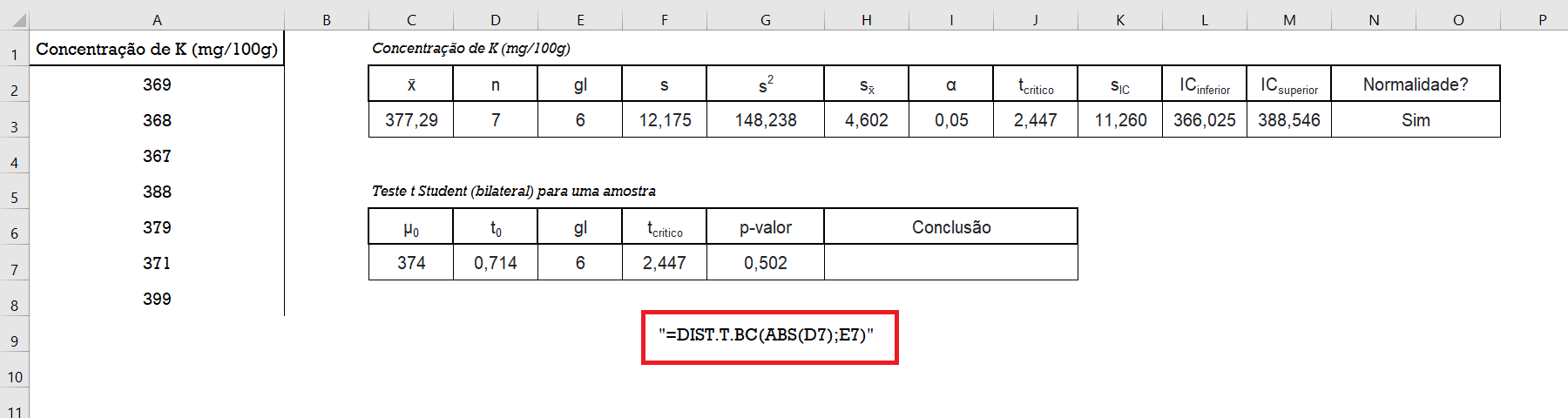
Dado que a estatística do teste ($t_{0}$) esta na célula D7 e que o grau de liberdade da amostra ($gl$) esta na célula E7, o $p-valor$ é obtido utilizando a seguinte fórmula:
=DIST.T.BC(ABS(D7);E7) 0,502
Conclusão
Comparando o valor crítico ($t_{critico}$) com a estatística do teste ($t_{0}$)
Podemos concluir o teste utilizando uma condição =SE(). Esta função recebe três parâmetros:
- O primeiro parâmetro é um teste lógico, onde vamos comparar o valor absoluto da estatística do teste com o valor crítico. Eu escolhi testar a condição em que rejeitamos a hipótese, pois é um intervalo aberto. Assim, ABS(t0)>t-critico.
- O segundo parâmetro corresponde ao valor que deve ser retornado caso a condição determinada no primeiro parâmetro seja VERDADEIRA. No caso onde $|t_{0}| > t_{critico}$ estamos rejeitando a hipótese nula. Logo, deve retornar “Rejeita H0”.
- O terceiro parâmetro corresponde ao valor que deve ser retornado caso a condição determinada no primeiro parâmetro seja FALSA. No caso onde $|t_{0}| \leq t_{critico}$ estamos aceitando a hipótese nula. Logo, deve retornar“Falha em rejeitar H0”.
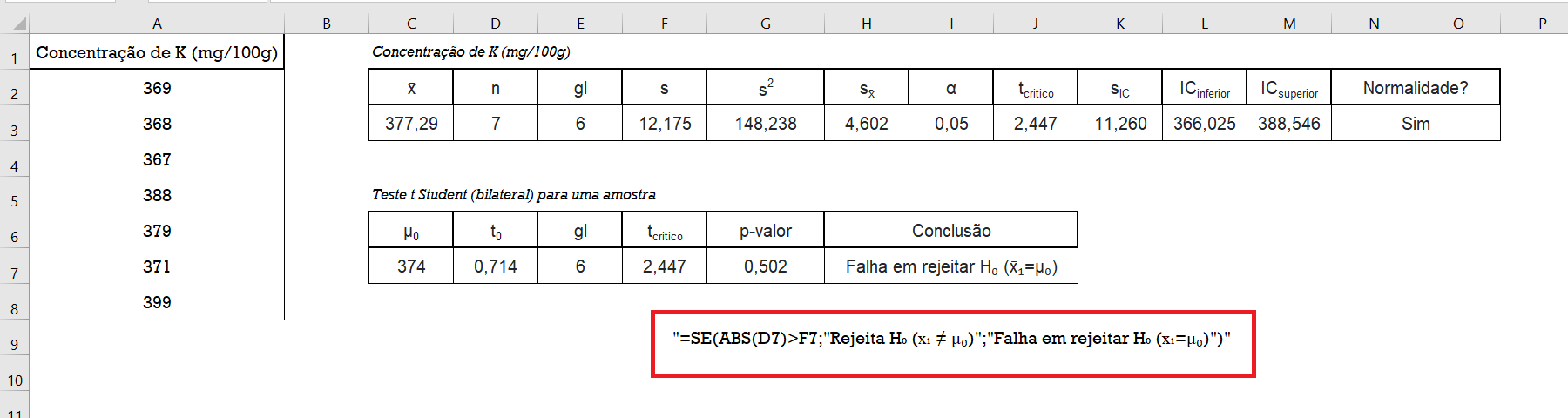
Dado que a estatística do teste ($t_{0}$) esta na célula D7 e que o valor crítico ($t_{critico}$) esta célula F7, a conclusão do teste é feita utilizando a seguinte fórmula:
=SE(ABS(D7)>F7;"Rejeita H₀ (x̄₁ ≠ μ₀)";"Falha em rejeitar H₀ (x̄₁=μ₀)") Falha em rejeitar H₀ (x̄₁=μ₀)
Comparando a probabilidade ($p-valor$) com o nível de significância adotado ($\alpha$)
Outra forma de concluir o teste é utilizando a probabilidade do teste, também utilizando uma condição =SE().
- O primeiro parâmetro é o teste lógico, onde vamos comparar o p-valor com o nível de significância adotado. Vamos testar a condição em que rejeitamos a hipótese nula que é um intervalo aberto. Assim, p-valor<alfa.
- O segundo parâmetro corresponde ao valor que deve ser retornado caso a condição seja aceita (VERDADEIRA). No caso onde $p-valor < \alpha$ estamos rejeitando a hipótese nula, que deve retornar “Rejeita H0”.
- O terceiro parâmetro corresponde ao valor que deve ser retornado caso a condição seja rejeitada (FALSA). No caso onde $p-valor \geq \alpha$ estamos aceitando a hipótese nula, que deve retornar“Falha em rejeitar H0”.
Dado que o $p-valor$ do teste esta na célula G7 e que o nível de significância adotado ($\alpha$) esta na célula I3, a conclusão do teste é feita utilizando a seguinte fórmula:
=SE(G7<I3;"Rejeita H₀ (x̄₁ ≠ μ₀)";"Falha em rejeitar H₀ (x̄₁=μ₀)")
Falha em rejeitar H₀ (x̄₁=μ₀) 
Conclusão geral
Neste artigo estudamos como aplicar o teste t para uma média com Excel. Infelizmente, o Excel não conta com uma função própria para este teste t. Felizmente, é simples de implementar um. Você pode baixar a planilha criada neste exemplo clicando neste link (você precisa estar logado em uma conta da Google).
Referências
STUDENT. The Probable Error of a Mean. Biometrika, v. 6, n. 1, p. 1, mar. 1908. DOI: https://doi.org/10.2307/2331554.
