Em um post recente nós estudamos com detalhes como aplicar o teste t de Student bilateral para comparar uma média, com distribuição Normal e variância desconhecida, com um valor esperado ou conhecido. Também já vimos como fazer estes cálculos utilizando a linguagem R e também com Excel. Neste artigo utilizamos outra a melhor linguagem de programação, e vamos aprender sobre como aplicar o teste t para uma média com Python! Aqui vamos focar apenas na aplicação do teste, mas caso você tenha dúvidas sobre o teste t, conjunto de dados e premissas adotadas, veja o post original.
Importações
As bibliotecas acima devem ser importadas para o ambiente Colab. É recomendado fazer isto logo nas primeiras linhas do código:
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt Entrada de dados
x = np.array([369, 368, 367, 388, 379, 371, 399])
mu_zero = 374
alpha = 0.05 # entre 0 e 1 Aplicando o teste
O teste de médias t de Student para uma amostra com variância desconhecida pode ser realizado utilizando a biblioteca SciPy (VIRTANEN, 2020). Nesta biblioteca temos a scipy.stats.ttest_1samp(), que aplica o teste (veja a documentação para detalhes específicos). Esta função deve receber pelo menos dois parâmetros:
- O primeiro é o conjunto de dados armazenado em um array.
- O segundo é o valor esperado armazenado como um número (int ou float).
Temos ainda o parâmetro alternative que controla qual é a hipótese alternativa do teste. Por padrão, alternative=”two-sided” que irá retornar o resultado para o teste bilateral. As outras são opções são “less” (teste unilateral à esquerda) ou “greater” (teste unilateral à direita). Como o padrão é “two-sided”, não precisamos passar o parâmetro alternative.
A função scipy.stats.ttest_1samp() retorna um object com diversos atributos. O atributo statistic contém a estatística do teste ($t_{0}$).
result = stats.ttest_1samp(x, mu_zero)
print(result.statistic)
>>> 0.7140011364639592 Cálculo do grau de liberdade
O objeto retornado da função scipy.stats.ttest_1samp() contém o atributo df que traz o gl do teste.
print(result.df)
>>> 6 Obtenção do valor crítico
Os valores críticos da distribuição t de Student podem ser obtidos com a função stats.stats.t.ppf() (veja maiores detalhes na documentação). Esta função recebe como primeiro parâmetro o nível de significância adotado e como segundo parâmetro ela recebe o grau de liberdade do teste. Porém, o nível de significância é unilateral. Por isto, devemos utilizar $1-\alpha/2$ para o obter o valor correto e positivo.
t_critico = stats.t.ppf(1-alpha/2, result.df)
print(t_critico)
>>> 2.4469118487916806 Obtenção do p-valor
O objeto retornado da função scipy.stats.ttest_1samp() contém o atributo pvalue que traz o p-valor do teste.
print(result.pvalue)
>>> 0.40978280474713114 Conclusão
Comparando o valor crítico ($t_{critico}$) com a estatística do teste ($t_{0}$)
Para concluir o teste utilizando Python basta criar uma lógica condicional if e else , seguindo os critérios determinados pelo teste.
if np.abs(result.statistic) > t_critico:
print(f"Rejeitamos a H₀ ({x.mean()} ≠ {mu_zero}, adotando {100*(1-alpha)}% de confiança )")
else:
print(f"Falhamos em rejeitar H₀ ({x.mean()} = {mu_zero}, adotando {100*(1-alpha)}% de confiança )")
>>> Falhamos em rejeitar H₀ (378.7142857142857 = 374, adotando 95.0% de confiança ) Comparando a probabilidade ($p-valor$) com o nível de significância adotado ($\alpha$)
De forma análoga ao utilizado acima, concluímos o teste seguindo os critérios determinados pelo teste:
if result.pvalue < alpha:
print(f"Rejeitamos a H₀ ({x.mean()} ≠ {mu_zero}, adotando {100*(1-alpha)}% de confiança )")
else:
print(f"Falhamos em rejeitar H₀ ({x.mean()} = {mu_zero}, adotando {100*(1-alpha)}% de confiança )")
>>> Falhamos em rejeitar H₀ (378.7142857142857 = 374, adotando 95.0% de confiança ) Gráfico da distribuição t de Student
odemos desenhar o gráfico da distribuição t de Student identificando a área referente ao $p-valor$, a estatística do teste ($t_{0}$) e o valor crítico ($t_{critico}$). Porém, é preciso criar uma função, que foi definida em student_two_side_plot(). Esta função deve receber quatro (4) parâmetros:
- axes : um instância de objeto matplotlib.axes.SubplotBase ;
- tcalc: a estatística do teste (float);
- gl: o grau de liberdade do teste (int);
- alpha: o nível de significância adotado (float).
Também podemos passar o parâmetro style, que controla o estilo do gráfico. Se style=None, o gráfico é desenhado colorido. Caso style=”grayscale”, o gráfico é desenhado em escala de cinza. Também é possível passar um dict com uma série de chaves que controlam cada elemento do gráfico.
A função retorna uma instância de matplotlib.axes.SubplotBase que pode ser adicionada em uma figura do matplotlib.
def student_two_side_plot(axes, tcalc, gl, alpha=0.05, style=None):
"""This function is experimental and its behavior may not be ideal.
"""
default_style = {
"dist_line_color": "k",
"dist_line_style": "-",
"critical_line_color": "b",
"critical_line_style": "--",
"marker_ecolor": "r",
"marker_facecolor": "r",
"fill_color": "salmon",
"fill_transparency": 0.5,
}
if style is None:
style = default_style
elif style == "grayscale":
style = {
"dist_line_color": "k",
"dist_line_style": "-",
"critical_line_color": "gray",
"critical_line_style": "--",
"marker_ecolor": "k",
"marker_facecolor": "white",
"fill_color": "lightgray",
"fill_transparency": 1,
}
else:
checkers._check_is_dict(style, "style")
if "dist_line_color" not in style.keys():
style["dist_line_color"] = default_style["dist_line_color"]
if "dist_line_style" not in style.keys():
style["dist_line_style"] = default_style["dist_line_style"]
if "critical_line_color" not in style.keys():
style["critical_line_color"] = default_style["critical_line_color"]
if "critical_line_style" not in style.keys():
style["critical_line_style"] = default_style["critical_line_style"]
if "marker_ecolor" not in style.keys():
style["marker_ecolor"] = default_style["marker_ecolor"]
if "marker_facecolor" not in style.keys():
style["marker_facecolor"] = default_style["marker_facecolor"]
if "fill_color" not in style.keys():
style["fill_color"] = default_style["fill_color"]
if "fill_transparency" not in style.keys():
style["fill_transparency"] = default_style["fill_transparency"]
t_critico = stats.t.ppf(1-alpha/2, gl)
if np.abs(tcalc) < t_critico:
x_lim = 6
else:
x_lim = np.abs(tcalc)*1.3
# criando valores para a distribuição t de Student com gl
x = np.linspace(-1*x_lim, x_lim, 1000)
y = stats.t.pdf(x, gl)
label = "$gl=" + str(gl) + "$"
axes.plot(x, y, c=style["dist_line_color"], ls=style["dist_line_style"], label=label)
# adicionando linhas com o valor crítico do teste
label= '$t_{tab}=' + str(round(t_critico, 2)) + '$'
axes.axvline(stats.t.ppf(1-alpha/2, gl), 0, 1, label=label, color=style["critical_line_color"], ls=style["critical_line_style"])
axes.axvline(stats.t.ppf(alpha/2, gl), 0, 1, color=style["critical_line_color"], ls=style["critical_line_style"])
# adicionando o valor da estatística do teste
label = "$t_{calc}=" + str(round(tcalc, 3)) + '$'
axes.scatter(tcalc, stats.t.pdf(np.abs(tcalc), gl), label=label, facecolor=style["marker_facecolor"], edgecolor=style["marker_ecolor"], s=50, zorder=10)
# preenchendo o lado esquero
x = np.linspace(-1*x_lim, -1*abs(tcalc), 1000)
pvalue = (1 - stats.t.cdf(np.abs(tcalc), gl))*2
if pvalue < 0.001:
label = "$pvalue<0.001$"
else:
label = "$pvalue=" + f"{round(pvalue, 3)}" + "$"
axes.fill_between(x, stats.t.pdf(x, gl), label=label, color=style["fill_color"], alpha=style["fill_transparency"])
# preenchendo o lado direito
x = np.linspace(abs(tcalc), x_lim, 1000)
axes.fill_between(x,stats.t.pdf(x, gl, loc=0, scale=1), color=style["fill_color"], alpha=style["fill_transparency"])
axes.set_xlim(-1*x_lim - .1, x_lim + .1)
axes.set_ylim(bottom=0.0)
axes.set_xlabel("$x$")
axes.set_ylabel("$Density$")
axes.legend(loc=1, fontsize=8)
return axes O gráfico pode ser desenhado utilizando as linhas abaixo.
fig, ax = plt.subplots(figsize=(8,4))
student_two_side_plot(axes=ax, tcalc=result.statistic, gl=result.df, alpha=alpha, style=None)
# plt.savefig("student-plot-t.png", bbox_inches='tight')
plt.show()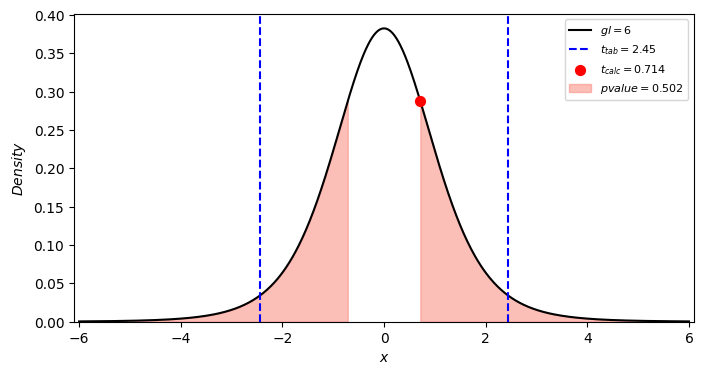 
Conclusão geral
Neste artigo vimos de forma bem prática como aplicar o teste t de Student bilateral para comparar uma média com um valor especificado utilizando Python. Os passos são relativamente simples, porém as etapas não são tão intuitivas como é no R. Porém, basta o pesquisador não ficar com receio de utilizar uma linguagem de programação que irá conseguir fazer este tipo de análise (e análises mais complexas).
Referências
VIRTANEN, P. et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods, v. 17, p. 261–272, 2020.
STUDENT. The Probable Error of a Mean. Biometrika, v. 6, n. 1, p. 1, mar. 1908. DOI: https://doi.org/10.2307/2331554.